SVM

Support Vector Machines

An Introduction

Introduction

Maximal Margin Hyperplane

Hard / Soft Margin

Non-linear Kernels

Overview

'G' to jump to slide. 'Ctrl+Shift+F' to search. 'Esc' to go to overview. 'S' for speaker view. 'Alt/Ctrl+Click' to zoom.

Introduction

Features and Key Concepts

Introduction

SVM is a supervised learning method primarily used for classifying two classes of data.

$y = 1$

$y = -1$

$S = \{(\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), \cdots, (\mathbf{x}_n, y_n)\}$

Learn

Supervised learning means that the class $y_i \in \{-1, 1\}$ for an $i$-th training sample $\mathbf{x}_i$ is known.

The decision boundary is learnt from training samples $S = \{(\mathbf{x}_i, y_i) \mid 1 \le i \le n \}$ to classify new data.

Optimal Margin

The decision boundary is a hyperplane that separates the two classes with the largest margin.

Wrong Hyperplane

Short Margin

Largest Margin

If the data is not linearly separable, the data needs to be transformed...

Kernels

A non-linear kernel transforms the data to higher dimensions where a hyperplane can be drawn.

Linear Kernel

A normal hyperplane in the data's feature space.

May underfit.

Non-linear Kernel (RBF)

Hyperplane in the kernel-mapped feature space.

May overfit.

The projection of the higher-dimensional hyperplane is a curved hypersurface in the original feature space.

With the right kernel, any data can be separated, but this causes overfitting when the true classifier is simple.

Hard vs. Soft Margins

Soft margins tolerate noise, allowing some training points to be misclassified.

Hard Margin

A hard margin fails if data cannot be separated.

Hence, kernel must overfit noisy data.

Soft Margin

A soft margin tolerates misclassifications.

An appropriate kernel can be used despite noisy data

As soft margins tolerate noise, a simple kernel can be used on noisy data, ensuring good generalisation.

Overview

In this course, we learn how to formulate a constrained optimization problem to find the hyperplane...

Margin

Maximum margin hyperplane

Constrained Optimization Problem

Lagrange formulation for finding hyperplane with the largest soft/hard margin

Primal

Dual

KKT

Support Vectors

Classification and hyperplane depend only on points which are support vectors

Kernel Trick

Reduces computation with non-linear kernels when classifying new points

Mercer's Condition

Gram Matrix

Kernel

... and understand how features like support vectors and the Kernel trick arises from the formulation.

Hyperplanes

Features and Key Concepts

Hyperplane (line in 2D-space): $\quad w_1x_1 + w_2x_2 + w_0 = 0$ Normal (always a line):
$\mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}$

Properties of Hyperplanes

Key to understanding SVM is the hyperplane equation, its normal...

Hyperplane Equation

$$ \mathbf{w}\cdot\mathbf{x} + w_0 \; = \; \mathbf{w}^\top \mathbf{x} + w_0 \; = \; \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_D \end{bmatrix}^\top \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_D \end{bmatrix} + w_0 \; = \; w_1 x_1 + w_2 x_2 + \cdots + w_0 \; = \; w_0 + \sum_{d = 1}^{D} w_d x_d \; = 0 $$

Any point $\mathbf{x} \in \mathbb{R}^D$ that lies on a ($D-1$) dimensional hyperplane characterised by the normal ($\mathbf{w}$) satisfies $\mathbf{w}^\top \mathbf{x} + w_0 = 0$.

Divides the $D$-dimensional feature space into two regions (half-spaces).

Normal

$\mathbf{w}$

Points in the direction $\mathbf{w}$ that is perpendicular to the hyperplane.

Vector

Scalar

2D plane in 3D space
3D hyperplane in 4D space

$\mathbf{w}^\top \mathbf{x} + w_0 \gt 0$ $\mathbf{w}^\top \mathbf{x} + w_0 = 0$ $\mathbf{w}^\top \mathbf{x} + w_0 \lt 0$ $\mathbf{w}$

Properties of Hyperplanes

Hyperplane Equation

$\mathbf{w}^\top \mathbf{x} + w_0 = 0$

Normal

$\mathbf{w}$

... and the relation of the normal to the perpendicular distance of any point

Perpendicular Distance

$$\frac{\left\lvert \mathbf{w}^\top \mathbf{x} + w_0 \right\rvert}{\lVert \mathbf{w} \rVert}$$

The shortest distance from $\mathbf{x}$ to the hyperplane.

$\mathbf{w}^\top \mathbf{x} + w_0 \gt 0$ if the point lies on the half-space pointed to by $\mathbf{w}$ from the hyperplane.

$\mathbf{w}^\top \mathbf{x} + w_0 \lt 0$ if the point lies on the half-space pointed to by $-\mathbf{w}$ from the hyperplane.

Properties of Hyperplanes

Scaling the hyperplane by multiplying $\mathbf{w}$ and $w_0$ by $c \in \mathbb{R}, c \ne 0$...

Scaling Invariance

Initial

Scaled

Hyperplane

$\mathbf{w}^\top \mathbf{x} + w_0 = 0$

$$ c\mathbf{w}^\top\mathbf{x} + c w_0 = 0 \implies \mathbf{w}^\top\mathbf{x} + w_0 = 0 $$

Points that are on the initial hyperplane remain on the scaled hyperplane. The two half-spaces are the same.

Normal

$\mathbf{w}$

$c \mathbf{w}$

The scaled normal is parallel to the original direction.

Perp. Distance

$$ \frac{\left\lvert \mathbf{w}^\top \mathbf{x} + w_0 \right\rvert}{\lVert \mathbf{w} \rVert} $$

$$ \frac{\lvert c \mathbf{w}^\top\mathbf{x} + c w_0 \rvert}{\lVert c \mathbf{w} \rVert} = \frac{\lvert c \rvert \lvert \mathbf{w}^\top \mathbf{x} + w_0 \rvert}{\sqrt{(c \mathbf{w})^\top(c \mathbf{w})}} = \frac{\lvert c \rvert \lvert \mathbf{w}^\top \mathbf{x} + w_0 \rvert }{\lvert c \rvert \sqrt{\mathbf{w}^\top\mathbf{w}}} = \frac{\lvert \mathbf{w}^\top \mathbf{x} + w_0 \rvert}{\lVert \mathbf{w} \rVert} $$

The perpendicular distance of any point to the hyperplane remains the same.

...does not change the hyperplane meaningfully.

Interactive Demo

Here's a demo to show that the perpendicular distance and hyperplane orientation is not affected by scaling.

Parameters

$w_1 =c w_1' = \;$

$w_2 =c w_2' = \;$

$w_0 =c w_0' = \;$

Perp. Dist.

$$\mathbf{w}^\top \mathbf{x}_i + w_0= \;$$

$$\frac{\lvert \mathbf{w}^\top \mathbf{x}_i + w_0 \rvert}{\lVert\mathbf{w}\rVert} = \; $$

Hyperplane Equation

$ f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} + w_0$ $ = 0$

HyperPlane

$w_1' \;$

$w_2' \;$

$w_0' \;$

$c\;$

Point

$x_{1,i}' \;$

$x_{2,i}' \;$

$\mathbf{w}^\top \mathbf{x} + w_0 \gt 0$

$\mathbf{w}^\top \mathbf{x} + w_0 \lt 0$

$\mathbf{w}$

$\mathbf{w}^\top \mathbf{x} + w_0 = 0$

Hyperplane Summary

Hyperplane Equation

$$\mathbf{w}^\top \mathbf{x} + w_0 = w_1x_1 + w_2x_2 + \cdots + w_Dx_D + w_0 = 0$$

Normal

$$\mathbf{w}$$

Perp Dist

$$\frac{\left\lvert \mathbf{w}^\top \mathbf{x} + w_0 \right\rvert}{\lVert \mathbf{w} \rVert}$$

Scale Invariance

Multiplying $\mathbf{w}$ and $w_0$ by $c$ does not change the hyperplane's orientation or any point's perpendicular distance to it.

1D line in $D=2$ space
2D plane in $D=3$ space
3D hyperplane in $D=4$ space

Margins

The Optimal Margin Classifier and the Geometric and Functional Margins

Optimal Margin Classifier

An unknown sample $\mathbf{x}_j$ can be very simply classified by comparing against $\mathbf{w}$...

Optimal / Maximal Margin Classfier

$\hat{y}_j = \mathrm{sgn} (\mathbf{w}^\top \mathbf{x}_j + w_0)$

...provided that $\mathbf{w}$ points in the direction of $y=1$ training samples.

For the learning process to know how to point to $y=1$ samples, we use margins.

The inferred class $\hat{y}_j$ of a sample $\mathbf{x}_j$ is the sign of $\mathbf{w}^\top \mathbf{x}_j + w_0$

Margins

Let the margins of a sample $\mathbf{x}_i$ be related to its label $y_i$ and its distance to the decision boundary:

Perp. Dist.

$$ \frac{\lvert \mathbf{w}^\top \mathbf{x}_i + w_0 \rvert }{\lVert \mathbf{w} \rVert} $$

Functional Margin $\hat{\gamma}_i$ of $\mathbf{x}_i$

$$ \hat{\gamma}_i = y_i (\mathbf{w}^\top \mathbf{x}_i + w_0) $$

Geometric Margin $\gamma_i$ of $\mathbf{x}_i$

$$ \gamma_i = \frac{y_i (\mathbf{w}^\top \mathbf{x}_i + w_0)}{\lVert \mathbf{w} \rVert} = \frac{\hat{\gamma}_i}{\lVert \mathbf{w} \rVert} $$

The margins of the set $S$ (all samples) are those of the samples with the smallest margins:

Functional Margin $\hat{\gamma}$

$$ \hat{\gamma} = \min_{i=1,\cdots,n} \hat{\gamma}_i $$

Geometric Margin $\gamma$

$$ \gamma = \frac{\hat{\gamma}}{\lVert \mathbf{w} \rVert}$$

Constrained Optimization #1

Formulating a constrained problem with Lagrange Multipliers

Convexity and Concavity: definition, examples, hessian

Gradient vector , tangent plane, level set.

Lagrange with one Constraint: Intuition.

Lagrange with multiple constraints: brief. (span of normals?)

SVM Optimization Problem

Formulating the constrained optimization problem w.r.t. margins and Lagrange Multipliers.

Naïve Optimisation Objective

To find the hyperplane with the largest margin, we can try to maximise the geometric margin $\gamma$...

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma \\ \mathrm{s.t.} & \quad \gamma > 0 \end{align*}$$

$$\gamma = \frac{\hat{\gamma}}{\lVert \mathbf{w} \rVert} = \frac{1}{\lVert \mathbf{w} \rVert} \min_{i=1,\cdots,n} y_i(\mathbf{w}^\top \mathbf{x}_i + w_0) $$

Potentially learns a $\mathbf{w}$ that points only to $y=1$ samples

$\gamma \gt 0 \implies \mathbf{w}$ points only to $y=1$ samples.
$\gamma \le 0 \implies \mathbf{w}$ can point to or away from any sample.

Maximise $\gamma$ by adjusting $w_0, w_1, \cdots, w_D$.

Naïve Optimisation Objective

...but this optimization problem does not have a solution.

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma \\ \mathrm{s.t.} & \quad \gamma > 0 \end{align*}$$

$$\gamma = \frac{\hat{\gamma}}{\lVert \mathbf{w} \rVert} = \frac{1}{\lVert \mathbf{w} \rVert} \min_{i=1,\cdots,n} y_i(\mathbf{w}^\top \mathbf{x}_i + w_0) $$

No unique $\mathbf{w}$

$\mathbf{w}$ and $w_0$ can be scaled to any value without changing the hyperplane's orientation or position.

Solved by constraining $w_0$ and $w$ to a fixed scale.

Objective is not concave

There is no global maximum, as the solution can reach $+\mathbf{\infty}$.

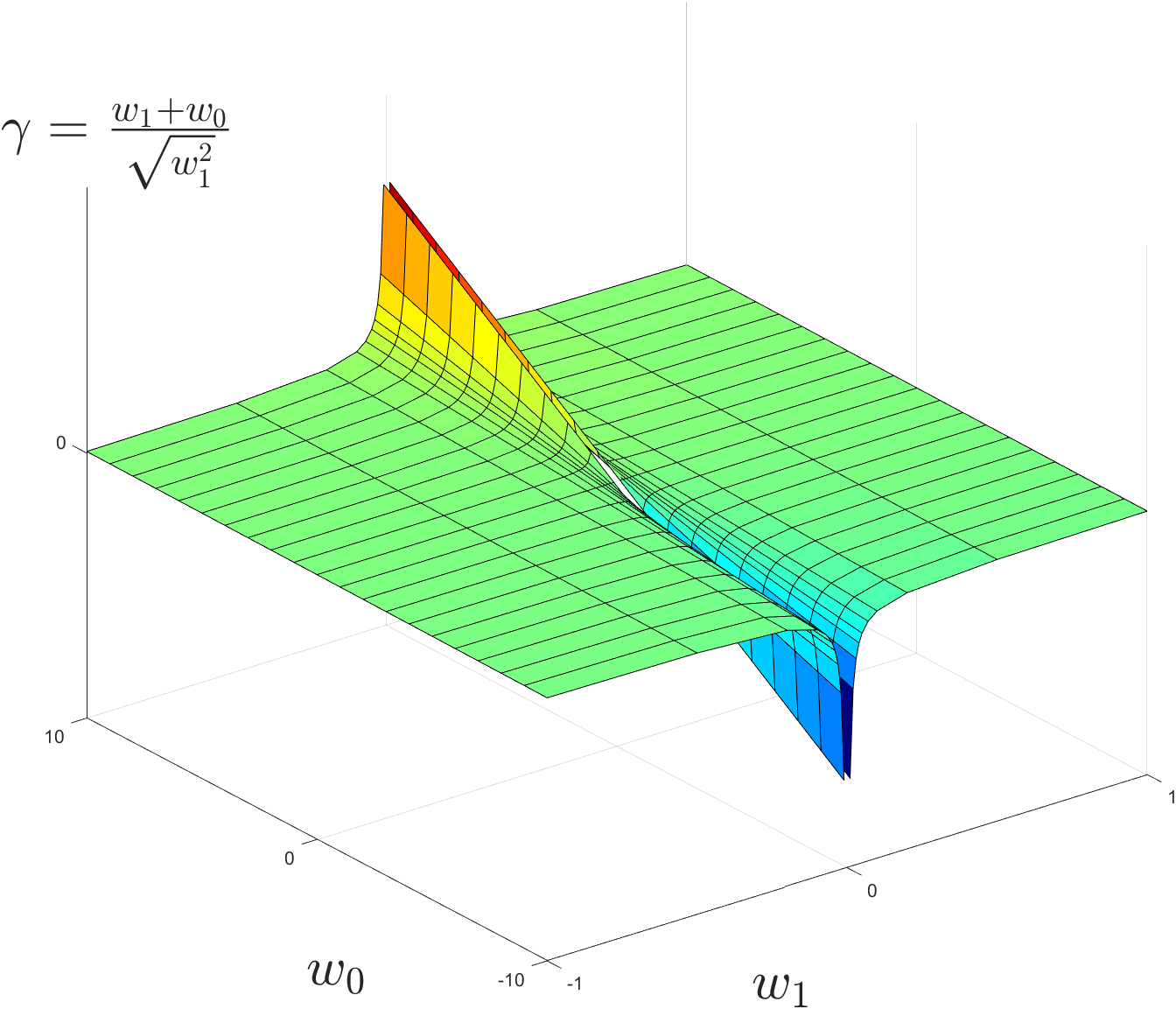
Have to refind a concave / convex objective.

Optimization Objective

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma \\ \mathrm{s.t.} & \quad \gamma > 0 \end{align*}$$

$$\gamma = \frac{\hat{\gamma}}{\lVert \mathbf{w} \rVert} = \frac{1}{\lVert \mathbf{w} \rVert} \min_{i=1,\cdots,n} y_i(\mathbf{w}^\top \mathbf{x}_i + w_0) $$

We first observe that scaling does not change our objective of maximising the geometric margin:

Scaled Geometric Margin $\gamma_c$

$$\gamma_c = \frac{\min_{i} y_i(c\mathbf{w}^\top \mathbf{x}_i + cw_0) }{\lVert c\mathbf{w} \rVert} = \frac{c\hat{\gamma}}{\lvert c \rvert \; \lVert \mathbf{w} \rVert} = \frac{c}{\lvert c \rvert}\gamma = \gamma\,\mathrm{sgn}(c) $$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma_c \\ \mathrm{s.t.} & \quad \gamma_c > 0 \end{align*}$$

$\equiv$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma \\ \mathrm{s.t.} & \quad \gamma > 0 \end{align*}$$

Optimization Objective

Scaled Geometric Margin $\gamma_c$

Thus, the numer. or denom. can be constrained to an arbitrary $k\ne 0$, and we can max. what's left:

Constrain Denominator

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma_c \\ \mathrm{s.t.} & \quad \gamma_c \gt 0, \\ & \quad \lvert c \rvert \; \lVert \mathbf{w} \rVert = k \end{align*}$$

$\equiv$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \frac{c \hat{\gamma}}{k} \\ \mathrm{s.t.} & \quad \frac{c \hat{\gamma}}{k} \gt 0, \\ & \quad \lvert c \rvert \; \lVert \mathbf{w} \rVert = k \end{align*}$$

$\equiv$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \hat{\gamma} \\ \mathrm{s.t.} & \quad \hat{\gamma}\gt 0, \\ & \quad \lVert \mathbf{w} \rVert = k' \end{align*}$$

Constrain Numerator

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma_c \\ \mathrm{s.t.} & \quad \gamma_c \gt 0, \\ & \quad c \hat{\gamma} = k \end{align*}$$

$\equiv$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \frac{k}{\lvert c \rvert \; \lVert \mathbf{w} \rVert} \\ \mathrm{s.t.} & \quad \frac{k}{\lvert c \rvert \; \lVert \mathbf{w} \rVert} \gt 0, \\ & \quad c \hat{\gamma} = k \end{align*}$$

$\equiv$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \frac{1}{\lVert \mathbf{w} \rVert} \\ \mathrm{s.t.} & \quad \frac{1}{\lVert \mathbf{w} \rVert} \gt 0, \\ & \quad \hat{\gamma} = k' \end{align*}$$

This helps us to simplify the problem, so we may find a concave / convex objective.

Optimization Objective

Thus, the numer. or denom. can be constrained to an arbitrary $k\ne 0$, and we can max. what's left:

Constrain Denominator

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma_c \\ \mathrm{s.t.} & \quad \gamma_c \gt 0, \\ & \quad \lvert c \rvert \; \lVert \mathbf{w} \rVert = k \end{align*}$$

$\equiv$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \hat{\gamma} \\ \mathrm{s.t.} & \quad \hat{\gamma}\gt 0, \\ & \quad \lVert \mathbf{w} \rVert = k' \end{align*}$$

Constrain Numerator

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \gamma_c \\ \mathrm{s.t.} & \quad \gamma_c \gt 0, \\ & \quad c \hat{\gamma} = k \end{align*}$$

$\equiv$

$$\begin{align*} \max_{\mathbf{w}, w_0} & \quad \frac{1}{\lVert \mathbf{w} \rVert} \\ \mathrm{s.t.} & \quad \frac{1}{\lVert \mathbf{w} \rVert} \gt 0, \\ & \quad \hat{\gamma} = k' \end{align*}$$

This helps us to simplify the problem, so we may find a concave / convex objective.

Constrained Optimization #2

Primal and Dual Lagrange Formulations

Primal: maximise multiplier than minimise w.

Primal: multipliers act like barrier functions that tends to inf when constraints violated. left with w if constraints satisfied.

Dual: minimise w than maximise w.

Dual: show that dual is le primal due to constraints.

Dual: gain insights to problem. not faster when a lot of samples.